le frequenze delle note musicali – what are the frequencies of music notes?
Qui di seguito sono riportate due pagine che illustrano formule atte a calcolare le frequenze dell varie note musicali prendendo come riferimento la nota la a 440 hz.
Per un calcolo delle frequenze per la scala pitagorica, o temperamento pitagorico (riferimento nota la = 432 hz), sostituire il valore 440 dell’equazione con il valore 432.
THX
A note 432 hz info (english language) — http://en.wikipedia.org/wiki/Pythagorean_tuning
—
fonte http://ulisse.sissa.it/chiediAUlisse/domanda/2004/Ucau040418d001/
Le frequenze delle note musicali
Stabilito che la nota musicale La della ottava centrale corrisponde a una frequenza di 440 Hz e che il rapporto tra le frequenze della stessa nota nella ottava superire (inferiore) è 1:2, esiste una formula per calcolare la frequenza di tutte le altre note, compresi i semitoni, delle ottave del pianoforte?
Alessio Zavaldi
18 aprile 2004
La domanda fa implicitamente riferimento all’accordatura temperata, ossia a quella abitualmente oggi in uso, e a questa mi limito.
La formula (che andrebbe spiegata nella sua genesi, ma questo non viene chiesto nella domanda) è questa:
2n/12· f (rif)
ossia 2 elevato a n/12 e moltiplicato per la frequenza della nota di riferimento, dove n è il numero dei semitoni di distanza dalla nota di riferimento stessa.
Ad esempio: rispetto al La a 440 Hz, la frequenza del Si, che dista dal La due semitoni, è
22/12· 440 = 1,1225 · 440 = 493,9
Sempre con riferimento al La a 440 Hz, le frequenze delle note dell’ottava centrale del pianoforte sono:
| Do | 261,6 Hz |
| Do # = Re b | 277,2 Hz |
| Re | 293,7 Hz |
| Re # | 311,1 Hz |
| Mi | 329,6 Hz |
| Fa | 349,2 Hz |
| Fa # | 370,0 Hz |
| Sol | 392 Hz |
| Sol # | 415,3 Hz |
| La | 440 Hz |
| La # | 466,2 Hz |
| Si | 493,9 Hz |
| Do | 523,3 Hz |
Gianni Zanarini Dipartimento di Fisica, Università di Bologna
Keywords: letteratura e scienza, sistemi complessi, acustica, musica e scienza
—
source http://www.intmath.com/trigonometric-graphs/music.php
What are the frequencies of music notes?

In the table of frequencies below, you’ll find A = 440 Hz, and then
A# = 466.16 Hz,
B = 493.88 Hz,
C = 523.25 Hz, etc.
Also, you can find Middle C: 261.63 Hz.
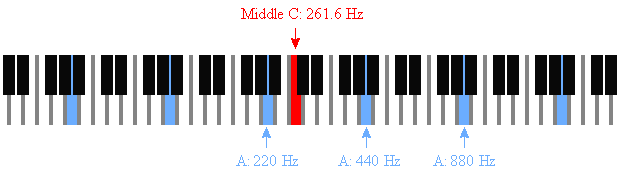
Table of Musical Frequencies
| DO2 | C2 | 66 Hz |
| DO#2 | C#2 | 70 Hz |
| RE2 | D2 | 74 Hz |
| RE#2 | D#2 | 78 Hz |
| MI2 | E2 | 83 Hz |
| FA2 | F2 | 88 Hz |
| FA#2 | F#2 | 93 Hz |
| SOL2 | G2 | 98 Hz |
| SOL#2 | G#2 | 104 Hz |
| LA2 | A2 | 110 Hz |
| LA#2 | A#2 | 117 Hz |
| SI2 | B2 | 124 Hz |
| DO3 | C3 | 131 Hz |
| DO#3 | C#3 | 139 Hz |
| RE3 | D3 | 147 Hz |
| RE#3 | D#3 | 156 Hz |
| MI3 | E3 | 165 Hz |
| FA3 | F3 | 175 Hz |
| FA#3 | F#3 | 185 Hz |
| SOL3 | G3 | 196 Hz |
| SOL#3 | G#3 | 208 Hz |
| LA3 | A3 | 220 Hz |
| LA#3 | A#3 | 233 Hz |
| SI3 | B3 | 247 Hz |
| DO4 | C4 | 262 Hz |
| DO#4 | C#4 | 277 Hz |
| RE4 | D4 | 294 Hz |
| RE#4 | D#4 | 311 Hz |
| MI4 | E4 | 330 Hz |
| FA4 | F4 | 349 Hz |
| FA#4 | F#4 | 370 Hz |
| SOL4 | G4 | 392 Hz |
| SOL#4 | G#4 | 415 Hz |
| LA4 | A4 | 440 Hz |
| LA#4 | A#4 | 466 Hz |
| SI4 | B4 | 494 Hz |
| DO5 | C5 | 523 Hz |
| DO#5 | C#5 | 554 Hz |
| RE5 | D5 | 587 Hz |
| RE#5 | D#5 | 622 Hz |
| MI5 | E5 | 659 Hz |
| FA5 | F5 | 698 Hz |
| FA#5 | F#5 | 740 Hz |
| SOL5 | G5 | 784 Hz |
| SOL#5 | G#5 | 831 Hz |
| LA5 | A5 | 880 Hz |
| LA#5 | A#5 | 932 Hz |
| SI5 | B5 | 988 Hz |
| DO6 | C6 | 1046 Hz |
| DO#6 | C#6 | 1109 Hz |
| RE6 | D6 | 1175 Hz |
| RE#6 | D#6 | 1245 Hz |
| MI6 | E6 | 1319 Hz |
| FA6 | F6 | 1397 Hz |
| FA#6 | F#6 | 1480 Hz |
| SOL6 | G6 | 1568 Hz |
| SOL#6 | G#6 | 1661 Hz |
| LA6 | A6 | 1760 Hz |
| LA#6 | A#6 | 1865 Hz |
| SI6 | B6 | 1976 Hz |
| DO7 | C7 | 2093 Hz |
| DO#7 | C#7 | 2217 Hz |
| RE7 | D7 | 2349 Hz |
| RE#7 | D#7 | 2489 Hz |
| MI7 | E7 | 2637 Hz |
| FA7 | F7 | 2794 Hz |
| FA#7 | F#7 | 2960 Hz |
| SOL7 | G7 | 3136 Hz |
| SOL#7 | G#7 | 3322 Hz |
| LA7 | A7 | 3520 Hz |
| LA#7 | A#7 | 3729 Hz |
| SI7 | B7 | 3951 Hz |
| DO8 | C8 | 4186 Hz |
These are found using
frequency = 440×(2n/12)
for n = -21, -19, …, 27
Where did this formula come from?
This problem reminded me of Compound Interest that we met earlier in Money Math. The frequency needs to double every 12 notes (because there are 7 white notes and 5 black notes in each octave.)
Here is a graph of that relationship: frequency = 440×(2n/12)
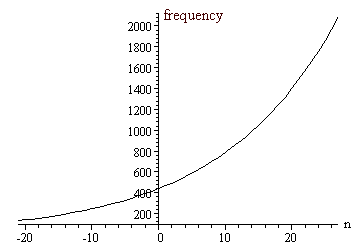
This is an exponential curve, that we met earlier in Graphs of Exponential Functions.
Equal Tempered Tuning
An interesting problem has faced musical instrument makers for hundreds of years. To get a “perfect 5th” (the interval between A and the E above, say), we need to play a note which has 1.5 times the frequency of A.
On a violin (or viola or any fretless stringed instrument) this is possible, and we can play a beautiful, perfect E at 440 × 1.5 = 660 Hz. But notice (from the frequency table above) that a piano playing the same note will play E = 659.26 Hz [just a little flat!].
Around 400 years ago, keyboards (usually harpsichords and organs) were tuned for a particular key (say D major), so that all the instruments, especially strings, sounded “right” in that key. The harpsichord sounded great in that key, but pretty awful in other unrelated keys (say B flat).
Around the time of J. S. Bach, it was decided to tune keyboards so that the notes were evenly spaced. Then the keyboard could sound better in any key. This is called equal tempered tuning.
Unfortunately, it means all stringed instruments have to allow for the slight differences in tunings between instruments. Strings are usually happiest when playing with other strings only, for this reason.